Relations et classes d'équivalence

Relations et ensembles

On considère des relations entre l’ensemble $A=\{1,3,5,7\}$ et l’ensemble $B=\{3,4,5,6\}$. Écrire les relations suivantes comme des sous ensembles de $A\times B$.

1. « est inférieur strictement à »,
2. « est inférieur ou égal à »,
3. « divise ».

Écrire les relations réciproques de chacune des relations précédentes.

---

Dessiner les graphes des fonctions suivantes et de leurs inverses.

1. La fonction $f : \mathbb{N} \to \mathbb{N}$ définie par $f(x) = x$.
2. La fonction $f : \mathbb{N} \to \mathbb{N}$ définie par $f(n) = 2n$ ;
3. La fonction $f : \mathbb{R} \to \mathbb{R}$ définie par $f(x) = 1/x$ ;

On rappelle qu’un graphe est une relation. Dans les cas ci-dessus, s’agit-il de relations réflexives, symétriques, transitives ?

Diagrammes de Hasse

Considérons le graphe de compatibilité des groupes sanguins: $x \to y$ signifie que une personne du groupe sanguin $x$ peut donner son sang à une personne du groupe sanguin $y$.

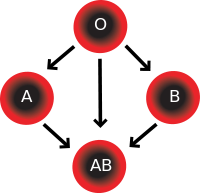
Définir la relation « compatibilité ». Est-elle réflexive, transitive, symétrique, antisymétrique?

---

Rappel : l’ensemble des parties d’un ensemble $A$ est l’ensemble de tous les sous-ensembles de $A$ (y compris l’ensemble vide et $A$ lui-même).

On considère l’ensemble des parties de $A=\{1,2,3\}$ muni de la relation $x \subset y$ ($x$ est contenu dans $y$). La relation $\subset$ est-elle un ordre ? En dessiner le diagramme de Hasse.

Propriétés des relations

Donner des exemples de relations qui sont

1. réflexives et symétriques mais pas transitives,
2. réflexives et transitives mais pas symétriques,
3. symétriques et transitives mais pas réflexives.

---

La relation sur les entiers suivante est-elle une relation d’équivalence ?

$\mathcal{T} = \{(a, b) \;\vert\; a + b \text{ est pair}\}$.

Donner la classe d’équivalence de 3, 4, 5, 6.

---

Les relations suivantes sont-elles des relations d’ordre sur les entiers? Et sur les rationnels?

1. $x\mathcal{P}y$ si et seulement si $x \le y$.
2. $x\mathcal{Q}y$ si et seulement si $x < y$.
3. $x\mathcal{R}y$ si et seulement si $x$ est multiple de $y$.
4. $x\mathcal{S}y$ si et seulement si l’écriture de $x$ en base dix est contenue dans l’écriture de $y$ en base dix (ex. : $101\;\mathcal{S}\;31012$).

---

Rappel: On dit que $a \equiv b \mod n$, et on lit « $a$ équivaut à $b$ modulo $n$ », s’il existe une entier $q$ tel que $a - b = qn$. De façon équivalente, $a\equiv b\mod n$ si $a$ et $b$ donnent le même reste dans la division par $n$.

Montrer que pour tout entier $n$, la relation « équivalent modulo $n$ » est une relation d’équivalence sur les entiers. Caractériser les classes d’équivalence.

---

Soit $E = \{1, 2, 3, 4, 5, 6, 7, 8\}$. On définit sur l’ensemble $E \times E$ la relation $\mathcal{R}$: $(p, q)\mathcal{R}(p', q')$ si et seulement si $p - p'$ est pair et $q - q'$ est divisible par 3.

1. Donner le cardinal de $E \times E$.
2. Vérifier que $\mathcal{R}$ est une relation d’équivalence.

On désigne par $\overline{(p, q)}$ la classe d’équivalence de $(p, q)$.

1. Calculer le nombre d’éléments des classes $\overline{(1, 1)}, \overline{(1, 2)}, \overline{(1, 3)}$.
2. Soit $q \in E$. Montrer que si $(x, y) \in \overline{(1, q)}$, alors $(x + 1, y) \in \overline{(2, q)}$.
3. Combien y a-t-il de classes d’équivalence différentes ? Donner leur liste.
4. Déterminer le cardinal de chaque classe d’équivalence. Le résultat est-il compatible avec la cardinalité de $E\times E$?